在超级云计算、工业互联网大数据中心等为代表的新型基础设施建设的推动下，数字化社会的发展对有线和无线接入带宽的需求呈现爆炸式增长。光纤的衰减系数和有效面积是大容量、长距离、高速率传输的关键因素。G.654.E光纤具有更低的衰减系数，可以延长传输距离，减少中继站数量，降低建设成本；更大的有效面积，可以提高入纤光功率，降低非线性效应，是400G、800G及未来Tbit/s超高速传输技术的首选光纤。测试数据表明，对于速率将升级为400G的干线，G.654.E光纤可望提升传输距离60%～80%，节省20%的光中继站数量、50%的电中继站数量，降低30%的站点能耗。由此可见，G.654.E光纤的更广泛使用是大势所趋。

本文从光纤损耗机理展开，从光纤瑞利散射、密度波动及拉丝工艺等因素出发，阐述光通信用超低损耗大有效面积G.654.E光纤的制造。

1 光纤衰减机理

光在光纤中传输光能衰减损耗的机理是材料本身吸收损耗、制造缺陷的不均匀引起的散色损耗、弯曲辐射损耗、连接损耗等对光能的吸收、散色损耗。通常，可以用下列方程表征光纤衰减的产生机理。

式中，是一个常数，它是瑞利散射造成的衰减；也是一个常数，它是由光纤结构不完善引起的衰减；是一个波长的函数，它描述由光纤杂质吸收衰减。图1形象地描述了光纤中光损耗的产生机理。

图1 光纤中光损耗产生的机理和分类

2 瑞利散射

瑞利散射起源于材料内部的微小随机起伏，这种密度的起伏导致介质内部折射率在空间上的微小随机起伏，并进而产生对介质内部传输光场的散射作用，引起光能量的损失。对瑞利散射现象的理论分析需要对材料内的密度起伏进行恰当的统计描述才能得到。理论分析和实验研究结果表明，无论是气体、液体还是固体介质，介质内由瑞利散射所引起的功率散失与光波长的四次方成反比。在熔融石英光纤低损耗窗口附近，由瑞利散射所引起的光损耗为：

根据上式，在OH^-等杂质浓度被充分降低的情况下，瑞利散射损耗是石英光纤低损耗窗口内最主要的损耗来源。由于瑞利散射是不可避免的，因此瑞利散射损耗是光纤所能达到的最低理论极限。

式中，常数C的大小范围是0.7~0.9，与光纤纤芯的组成有关。在1.55μm波长对应的衰减为0.12~0.16dB/km。这说明，在1.55μm波长附近，光纤的衰减主要由瑞利散射所决定。

单模光纤中的衰减瑞利散射占80%，对于石英光纤而言，瑞利散射可以分为密度波动和浓度波动，因此降低光纤衰减主要的方向就是降低瑞利散射中的浓度波动和密度波动。

密度波动带来的瑞利散射可表示为：

式中，λ为波长，n为折射率，p为Pockel光弹系数（1.38*10^-23 JK^-1），k为玻尔兹曼常数，T_f为假想温度，β_T为等温压缩率。

引起光纤瑞利散射衰减的另一个重要原因是化学成分的不均匀，即浓度波动。对于玻璃内进行GeO₂和F掺杂的单模光纤而言，由掺杂浓度波动（化学成分不均匀）带来的瑞利散射可表示为：

与瑞利散射的基本性质相同，密度波动和浓度波动都与波长的四次方成反比。值得注意的是，密度波动引起的瑞利散射与石英玻璃的假想温度成正比，因此降低材料体系的假想温度有利于降低瑞利散射。

3 假想温度

石英玻璃的假想温度是指玻璃液态冷却到平衡态的温度。不同的冷却速率将产生不同的后果。当玻璃在软化温度T_s点长时间缓慢冷却时，将会结晶成为石英晶体。相反，如果在这个温度下快速冷却，液态玻璃将不会结晶化，而成为过冷液体。过冷液体缓慢冷却时，在转变点温度T_g下转化为固体；而快速冷却时，则在假想温度T_f下转化为固体玻璃。

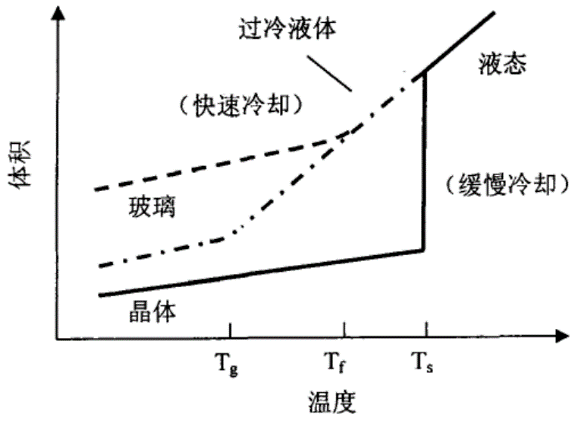
图2 玻璃在冷却过程中的体积变化示意图

需要说明的是，在拉丝过程中，光纤材料内部的密度不均匀并非由环境温度决定，而是由玻璃的假想温度（fictive temperature）所决定。假想温度为玻璃材料由液态（软化状态）向固态的转变温度T_f。由图2所示。

理论上，瑞利散射系数和假想温度成正比，这一点已经被Tsujikawa等人证实。通过改变熔融温度，得到不同假想温度的SiO₂和Ge掺杂SiO₂样品，并得到假想温度与瑞利散射的线性关系。研究表明随着假想温度从1700℃下降到1200℃，瑞利散射系数降低了（15±2）%。

结合密度波动公式（3），从光纤拉丝工艺考虑，降低假想温度是降低光纤瑞利散射有效的方法。而光纤的假想温度与拉丝炉温度、拉丝速度等拉丝条件密切相关，由冷却速率和玻璃黏度决定。对特定的光纤而言，光纤预制棒的种类、结构、黏度等条件都是固定的，假想温度主要取决于拉丝速率，二者的关系可表示为：

式中，a₁、a₂为材料常数，q、q₀为冷却速率，q₀=1K/s。从公式分析得到，降低冷却速率是降低光纤假想温度的有效方法。

3.1红外光谱法

石英玻璃的红外反射光谱中，1122cm^-1谱带归属于玻璃结构中的Si-O-Si键的伸缩振动，该谱带的位置与石英玻璃的结构及其各种物化性质直接关联。通过测量该谱带位置v₁来确定石英玻璃表面的假想温度，从而度量其表面结构弛豫。同时，石英玻璃的红外吸收光谱中，2260cm^-1谱带归属于[SiO₄]基频振动的第一倍频。通过测量此谱带位置v₂来表征石英玻璃体相结构弛豫和假想温度。

红外反射光谱的计算公式：

红外吸收光谱的计算公式：

3.2拉曼光谱法

拉曼光谱在800cm^-1处表现出宽的ω₃峰，这归因于二氧化硅玻璃固有的Si-O-Si变形振动，在605 cm^-1处呈现出窄的D2峰，这归功于引起密度波动的3元环的拉伸振动。可以通过计算峰面积比D2/ω3来量化密度波动的程度。密度波动程度可以由虚拟温度表示，该虚拟温度被定义为具有相同密度波动程度的SiO₂的平衡液态的温度。因此，通过使用已知假想温度的二氧化硅玻璃样品测量上述D₂/ω₃比率，建立D₂/ω₃比值-Tf -衰减的标准曲线，可以通过测量未知样品的D₂/ω₃比率来确定其假想温度。

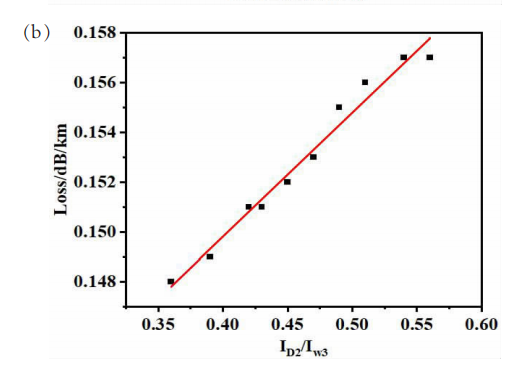
图3 a石英光纤的拉曼光谱图；b光纤1550nm衰减和D2/ω3比值的关系趋势

4 光纤设计与验证

光纤中化学成分浓度不均匀主要是芯层掺杂元素Ge/F引起的。大有效面积G.654.E光纤中采用芯层微掺氟内外包深掺氟的光学结构，芯层微掺氟可以降低芯层的假想温度但不引起较大的浓度波动，内外包深掺氟是为了满足大有效面积的光学结构。另外，芯层微掺氟降低了芯层黏度，可以使芯层和内包层黏度更好地匹配，减少光纤拉丝过程中带来的缺陷。

表1超低损耗大有效面积G.654.E光纤光学性能

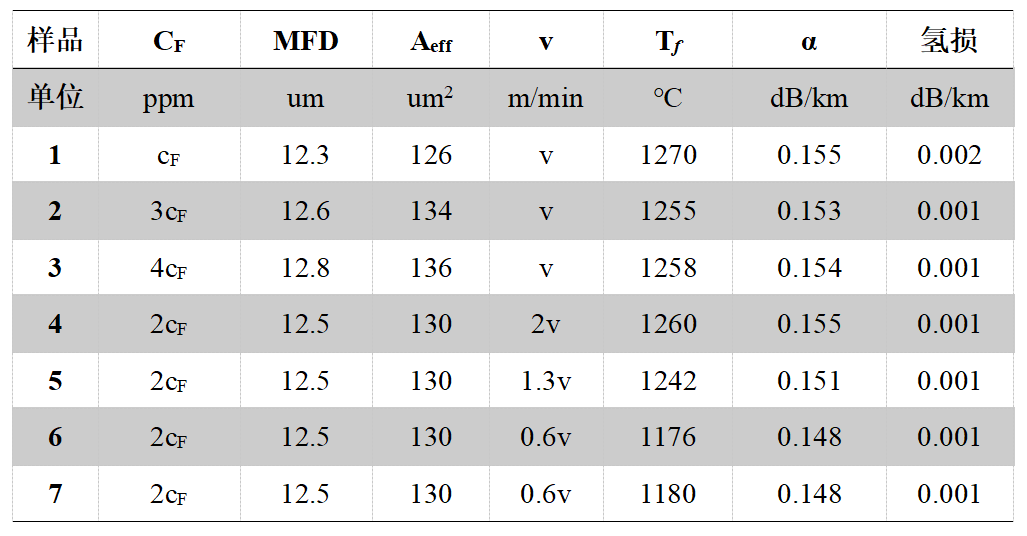
由表1所示，芯层F浓度分别掺杂c_F / 2c_F / 3c_F / 4c_F ppm，由于内包和外包折射率固定，芯层F浓度增加，光纤的MFD增大，有效面积增加，衰减呈现先降低后增长的趋势；拉丝速度分别为0.6v/v/1.3v/2v m/min，随着拉丝速度增加，衰减逐渐增加，当速度降低至v m/min后，1550nm衰减没有明显变化。因此，通过调节光纤预制棒芯层氟浓度和拉丝速度可以对光纤衰减进行调控，当掺F浓度为2c_F ppm，拉丝速度为v m/min时光纤1550nm衰减为0.148dB/km。

5 结论

本文通过对光纤衰减机理、瑞利散射的密度波动和浓度波动、假想温度测试方法等进行分析，介绍了通过芯层微掺氟工艺制备光纤预制棒，调控光纤拉丝速度来优化光纤衰减，进一步讨论了掺氟浓度和拉丝速度对超低损耗光纤衰减性能的影响，从而实现超低损耗大有效面积G.654.E光纤的制备。

(江苏亨通光纤科技有限公司  陈浩，张飞，李宝东，吕沛澴，刘金浩，宋鹏宇，劳雪刚)